Теория Фейгенбаума-Шарковского-Магницкого (ФШМ)

Во всех сложных нелинейных системах дифференциальных уравнений, описывающих многочисленные природные физические, химические, биологические, экологические, а также экономические и социальные процессы и явления макромира, включая диссипативные и консервативные, автономные и неавтономные системы, системы обыкновенных дифференциальных уравнений, уравнений с частными производными и запаздывающим аргументом, осуществляется единый универсальный бифуркационный сценарий усложнения динамики решений через каскад Фейгенбаума бифуркаций удвоения периодов устойчивых циклов или торов, затем через субгармонический каскад бифуркаций Шарковского рождения устойчивых циклов или торов любого периода вплоть до периода три в соответствии с порядком Шарковского

и затем через гомоклинический или гетероклинический каскад бифуркаций Магницкого устойчивых циклов или торов, сходящихся к соответствующим гомоклиническим или гетероклиническим сепаратрисным контурам или поверхностям.

Пример универсального сценария перехода к динамическому хаосу в двумерных неавтономных системах с периодическими коэффициентами через субгармонический каскад бифуркаций устойчивых циклов – обобщенное уравнение Матье (рис.1):

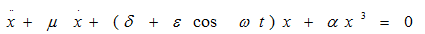
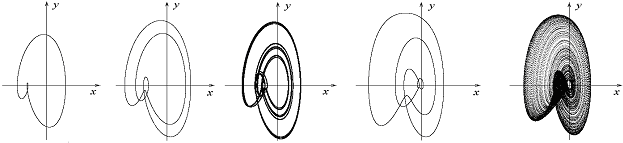
Рис.1. Сингулярный цикл, цикл периода 2, аттрактор Фейгенбаума, цикл периода 3, сингулярный циклический хаотический аттрактор.

Пример универсального сценария перехода к динамическому хаосу в автономных системах через субгармонический каскад бифуркаций устойчивых циклов – система уравнений Ресслера (рис.2):

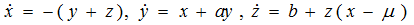
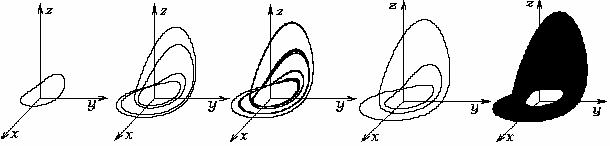
Рис.2. Сингулярный цикл, цикл периода 2, аттрактор Фейгенбаума, цикл периода 3, сингулярный циклический хаотический аттрактор.

Пример универсального сценария перехода к динамическому хаосу в системах уравнений с частными производными через субгармонический каскад бифуркаций устойчивых двумерных торов – уравнение Курамото-Цузуки (Гинзбурга-Ландау) (рис.3):

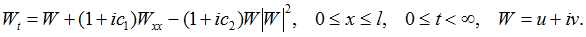
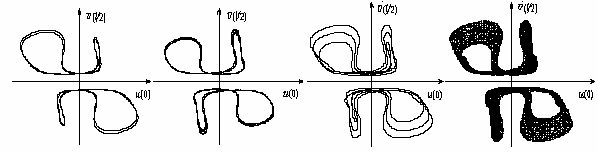
Рис.3. Проекции сечений сингулярного двумерного тора периода 2, тороидального аттрактора Фейгенбаума, двумерного тора периода 3, сингулярного тороидального хаотического аттрактора.

Пример универсального сценария перехода к турбулентности в системах уравнений с частными производными Навье-Стокса через субгармонический каскад бифуркаций устойчивых циклов и устойчивых двумерных торов – конвекция Рэлея-Бенара (рис.4):

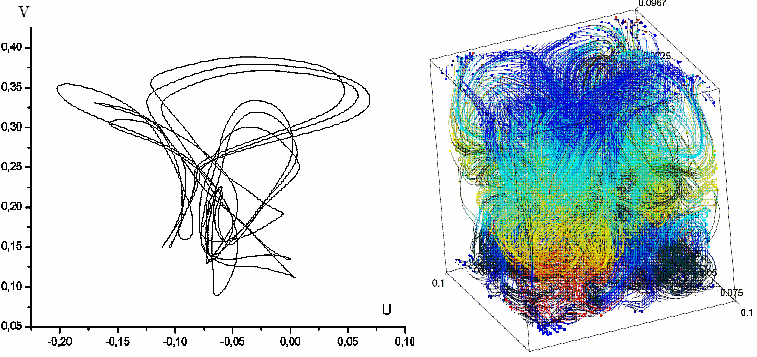
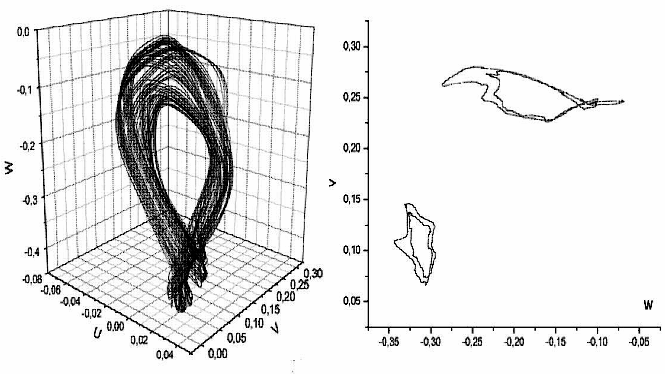
Рис.4. Проекция цикла периода три и соответствующий этому решению реальный турбулентный режим; двумерный тор периода два и проекция его сечения.

Публикации.

Универсальная теория динамического и пространственно-временного хаоса в сложных системах.

Изложены основы новой универсальной теории динамического и пространственно-временного хаоса в нелинейных системах дифференциальных уравнений, описывающих многочисленные сложные природные и социально-экономические процессы и явления, изучаемые математикой, физикой, химией, биологией, экономикой и другими науками. Продемонстрирована уникальная широта применимости новой теории к диссипативным и консервативным, автономным и неавтономным системам обыкновенных дифференциальных уравнений, к дифференциальным уравнениям с частными производными и с запаздывающим аргументом.

Теория динамического хаоса

В монографии изложена универсальная бифуркационная теория динамического хаоса во всех нелинейных системах дифференциальных уравнений: диссипативных и консервативных, автономных и неавтономных, обыкновенных, с частными производными и с запаздывающим аргументом, описывающих многочисленные сложные природные, научно-технические и социально-экономические явления и процессы. Решена проблема топологической структуры нерегулярных аттракторов диссипативных систем, разработана бифуркационная теория динамического хаоса в консервативных и гамильтоновых системах, создана бифуркационная теория пространственно-временного хаоса и турбулентности в системах уравнений с частными производными.

Все аналитические результаты и выводы подтверждены численными расчетами и проиллюстрированы многочисленными примерами реальных моделей физических, химических, биологических, экономических и социальных систем и процессов.

Книга предназначена для научных работников, аспирантов и студентов старших курсов, интересующихся проблемами хаотической динамики и устройством окружающего нас сложного нелинейного мира.