Электродинамика физического вакуума
Рассмотрим случай, когда скорость 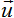 распространения возмущений в физическом вакууме имеет произвольное направление, задаваемое единичным вектором
распространения возмущений в физическом вакууме имеет произвольное направление, задаваемое единичным вектором
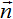 .
Решение системы уравнений физического вакуума будем искать в виде:
.
Решение системы уравнений физического вакуума будем искать в виде:
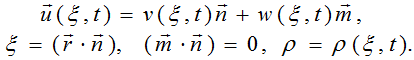
Для определения функций ρ(ξ,t),v(ξ,t),w(ξ,t) получим систему уравнений
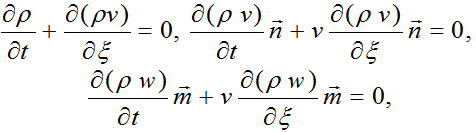
которую назовем системой уравнений электродинамики физического вакуума.
В частном случае поперечных колебаний физического вакуума постоянной плотности
(ρ(ξ,t)=ρ0=const)
и распространения этих колебаний в продольном направлении с постоянной скоростью v(ξ,t)=c
система уравнений электродинамики физического вакуума сводится к одному уравнению относительно одной комплексной переменной w(ξ,t)
Если теперь ввести в рассмотрение векторы напряженностей электрического 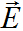 и магнитного
и магнитного 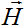 полей по формулам:
полей по формулам:
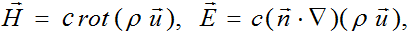
и применить к уравнению для функции w(ξ,t) последовательно операторы сrot и c(
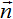 •∇)
то получим классическую систему уравнений Максвелла, описывающую
распространение электромагнитных волн в так называемой пустоте (вакууме)
•∇)
то получим классическую систему уравнений Максвелла, описывающую
распространение электромагнитных волн в так называемой пустоте (вакууме)
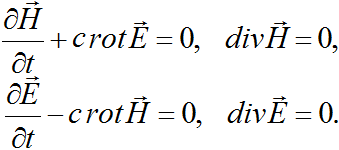
Решением системы уравнений Максвелла являются функции вида
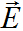 =
=
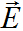 0
ei(ωt - kξ),
Принято считать, что физический смысл имеют вещественные части их
комплексных выражений, определяющие синфазную плоскую поперечную
электромагнитную волну, распространяющуюся со скоростью света c в произвольном направлении, задаваемом единичным вектором
0
ei(ωt - kξ),
Принято считать, что физический смысл имеют вещественные части их
комплексных выражений, определяющие синфазную плоскую поперечную
электромагнитную волну, распространяющуюся со скоростью света c в произвольном направлении, задаваемом единичным вектором
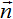 . Единственной характеристикой такой волны является ее частота
ω (или однозначно зависящая от нее длина волны λ=2πc/ω).
Заметим, что синфазные векторы напряженностей электрического и
магнитного полей периодически одновременно обращаются в нуль, что
противоречит закону сохранения энергии и вызывает сомнение в
справедливости классической интерпретации электромагнитной волны, при
которой изменение электрического поля вызывает изменение магнитного поля
и наоборот.
. Единственной характеристикой такой волны является ее частота
ω (или однозначно зависящая от нее длина волны λ=2πc/ω).
Заметим, что синфазные векторы напряженностей электрического и
магнитного полей периодически одновременно обращаются в нуль, что
противоречит закону сохранения энергии и вызывает сомнение в
справедливости классической интерпретации электромагнитной волны, при
которой изменение электрического поля вызывает изменение магнитного поля
и наоборот.
В свою очередь система уравнений электродинамики физического вакуума имеет своим решением спиральную волну w(ξ,t)
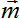 = (w * +
w0 ei(ωt - kξ))
= (w * +
w0 ei(ωt - kξ))
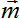 , ω = kс,
распространяющуюся со скоростью c в физическом вакууме в направлении вектора
, ω = kс,
распространяющуюся со скоростью c в физическом вакууме в направлении вектора 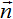 с сохранением переносимой волной энергии и имеющую произвольный постоянный сдвиг w*
в направлении вектора
с сохранением переносимой волной энергии и имеющую произвольный постоянный сдвиг w*
в направлении вектора 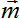 . В такой постановке скорость света c
в пустоте имеет ясный физический смысл - это скорость распространения
колебаний физического вакуума постоянной плотности при отсутствии
вещества (см. элементарные частицы). А так как в рассматриваемом случае векторы
. В такой постановке скорость света c
в пустоте имеет ясный физический смысл - это скорость распространения
колебаний физического вакуума постоянной плотности при отсутствии
вещества (см. элементарные частицы). А так как в рассматриваемом случае векторы 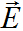 и
и
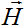 классической плоской электромагнитной волны являются производной по направлению и ротором
вектора ρ0w(ξ,t)
классической плоской электромагнитной волны являются производной по направлению и ротором
вектора ρ0w(ξ,t) 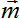 ,
то можно сделать вывод, что классическая электромагнитная волна
является искусственным образованием и полностью определяется спиральной
волной распространения возмущений в физическом вакууме (рис.1).
,
то можно сделать вывод, что классическая электромагнитная волна
является искусственным образованием и полностью определяется спиральной
волной распространения возмущений в физическом вакууме (рис.1).
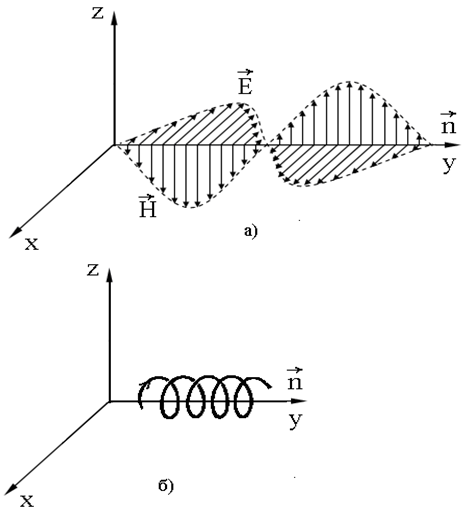
Рис.1. Распространение классической плоской электромагнитной волны (а) и спиральной волны физического вакуума (б).
Сравним спиральную волну в физическом вакууме, полученную из системы уравнений, инвариантной относительно преобразований Галилея, и классическую электромагнитную волну, полученную из системы уравнений Максвелла. Обе волны имеют произвольные частоты и соответствующие им длины волн, поэтому оба решения описывают все существующие в природе плоские поперечные электромагнитные колебания. Однако, как уже было отмечено выше, векторы классических электрического и магнитного полей являются искусственными векторами, а именно, производными одного и того же истинного вектора скорости распространения возмущений в физическом вакууме. В связи с этим среди решений системы уравнений Максвелла в принципе нет решений, отвечающих постоянному сдвигу w* поперечной волны физического вакуума. Это является основной причиной того, что уравнения Максвелла не инвариантны относительно преобразований Галилея, и, более того, их невозможно модифицировать таким образом, чтобы они оказались инвариантными относительно этих преобразований.
Кроме того, вид классической электромагнитной волны (рис. 1а) не дает возможности корректно определить понятие кванта электромагнитных колебаний (фотона), так как для этого кроме длины волны λ требуется также знание амплитуды колебаний. Вид спиральной волны распространения возмущений в физическом вакууме дает возможность однозначного определения фотона - это часть цилиндрического объема физического вакуума под спиралью волны длиной λ и радиусом r0=c/ω. Движение волны по спирали внутри данного объема происходит с постоянной угловой скоростью ω, а линейная скорость достигает своего максимального значения (скорости света c) на боковой поверхности цилиндра. Именно такой фотон, сталкиваясь с препятствием и сжимаясь, способен порождать элементарные частицы и античастицы в виде шаров радиуса r0(см. элементарные частицы).
Рассмотрим теперь общий случай распространения спиральных волн в
физическом вакууме переменной плотности. Применяя к сумме второго и
третьего уравнений системы уравнений электродинамики физического вакуума
последовательно операторы сrot, c
(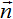 •∇) и вводя в рассмотрение линейную плотность заряда
ρch и плотность тока
•∇) и вводя в рассмотрение линейную плотность заряда
ρch и плотность тока 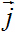 по формулам
по формулам
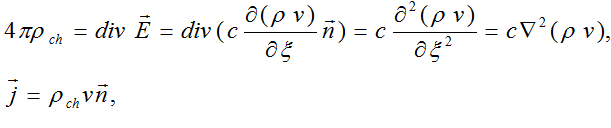
получим для векторов напряженностей электрического и магнитного полей систему уравнений
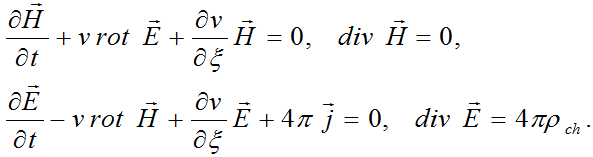
Заметим, что вектор напряженности электрического поля 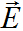 имеет отличную от нуля продольную составляющую даже в случае v=c=const,
при котором последняя система уравнений переходит в классическую
систему уравнений Максвелла в присутствии зарядов и токов. Отсюда
следует, что током в смысле классической системы уравнений Максвелла
является не движение зарядов, а вторая производная (оператор Лапласа) от
распространяющейся со скоростью света продольной волны периодических
сжатий-растяжений плотности физического вакуума, и что заряды и токи
могут существовать в физическом вакууме даже при отсутствии в нем
вещества (материи).
имеет отличную от нуля продольную составляющую даже в случае v=c=const,
при котором последняя система уравнений переходит в классическую
систему уравнений Максвелла в присутствии зарядов и токов. Отсюда
следует, что током в смысле классической системы уравнений Максвелла
является не движение зарядов, а вторая производная (оператор Лапласа) от
распространяющейся со скоростью света продольной волны периодических
сжатий-растяжений плотности физического вакуума, и что заряды и токи
могут существовать в физическом вакууме даже при отсутствии в нем
вещества (материи).
Таким образом, из справедливости постулата о существовании физического вакуума (эфира) следует, что: 1) уравнения Максвелла описывают распространение плоских электромагнитных волн в движущихся инерциальных системах отсчета только приближенно при малых скоростях движения таких систем относительно скорости света; 2) существуют более общие уравнения, выведенные из уравнений физического вакуума и законов классической механики, инвариантные относительно преобразований Галилея и точно описывающие распространение плоских электромагнитных волн в любых движущихся инерциальных системах отсчета; 3) выводы современной физики об абсолютизации системы уравнений Максвелла, о некорректности уравнений классической механики, а также основной постулат специальной теории относительности о постоянстве скорости света в любых инерциальных системах отсчета являются ошибочными.
- Никола Тесла
- Теория Фейгенбаума-Шарковского-Магницкого (ФШМ)
- Теория ЭДКВ Кирьяко
- Электродинамика физического вакуума
- Теория элементарных частиц
- Гравитация и гравитационные волны
- Автор: Магницкий Н.А



