Теория элементарных частиц

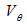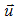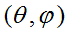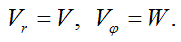Запишем систему уравнений динамики физического вакуума в сферических координатах и рассмотрим только такие решения полученной системы уравнений, у которых равна нулю компонента вектора скорости распространения возмущений по радиусу r и углам . Другие компоненты вектора скорости обозначим через В результате получим систему уравнений физики элементарных частиц:

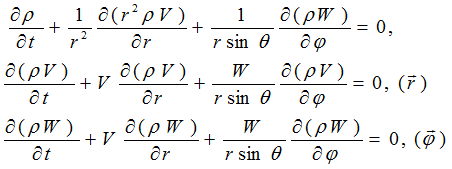
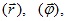В скобках после строк системы показаны единичные координатные векторы по которым направлены векторы соответствующих строк. Покажем, что полученная система уравнений имеет решения, обладающие при малых r всеми известными свойствами, присущими элементарным частицам. Эти решения будем искать в виде волн, распространяющихся с постоянной угловой скоростью по углу 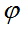под воздействием малых колебаний плотности физического вакуума:
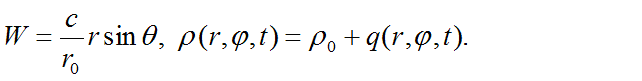
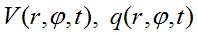Функции считаем малыми при малых r. При такой постановке каждая элементарная частица является шаром некоторого радиуса r0 , внутри которого вдоль любой параллели (окружности радиуса 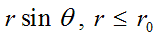) в результате малых колебаний плотности физического вакуума распространяются волны с постоянной угловой скоростью (частотой) c/r0, совершая полный обход параллели по углу 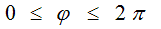за одинаковое время 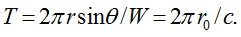Причем линейная скорость этих волн линейно растет с ростом радиуса, достигая своего максимального значения (скорости света с) на экваторе шара при (рис.1)
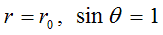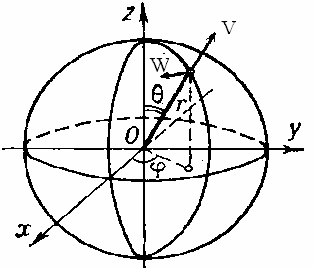
Рисунок 1
Рис.1. Схематическое изображение элементарной частицы.

Подставляя предполагаемый вид решений в систему уравнений физики элементарных частиц и пренебрегая членами второго порядка малости и произведениями малых членов, получим ее решения в виде

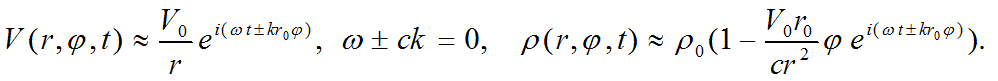
Заметим, что в таком приближении мы полностью пренебрегли существенно нелинейным членом второго порядка малости 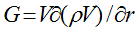. Именно этот член создает гравитационное поле частицы, но его роль становится значимой только при достаточно больших r.

Однако, не каждое из найденных таким образом волновых решение представляет собой элементарную частицу. Такое решение должно иметь электрическое поле и спин, обладать свойствами сохранения и универсальности заряда, квантованности массы, импульса и энергии. Кроме того, за время полного оборота волны вдоль экватора сферы напряженность электрического поля должна сохранять знак. Все эти классические и квантовомеханические понятия требуют корректных определений через характеристики физического вакуума.

В первую очередь дадим определения напряженности электрического поля и электрического заряда элементарной частицы по аналогии со случаем распространения плоских электромагнитных волн в электродинамике физического вакуума.

Определение. Напряженностью электрического поля 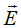и плотностью распределения заряда ρch элементарной частицы назовем следующие величины:


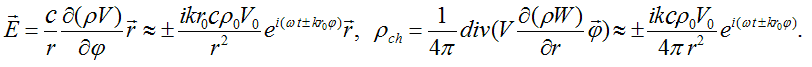
Заметим, что, как и в случае плоских электромагнитных волн, вектор напряженности электрического поля является лишь линеаризацией реального вектора поля 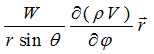и совпадает с ним только на экваторе сферы радиуса r0.

Вычислим заряд qch элементарной частицы, интегрируя стационарное распределение плотности заряда по шару радиуса r0:


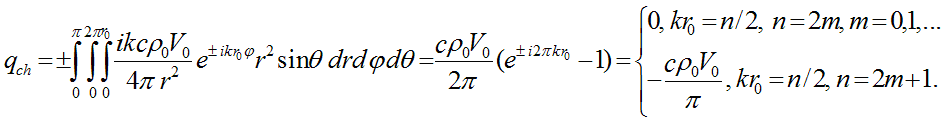
Из полученной формулы следует, что элементарным частицам соответствуют случаи целого или полуцелого волнового числа kr0 . Для целого числа kr0 заряд равен нулю, для любого полуцелого числа kr0 заряд равен единой по модулю универсальной величине 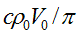, отрицательной при движении волны в сторону возрастания угла 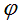(знак с положительный), и положительной при движении волны в противоположном направлении (знак с отрицательный). При этом время 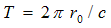полного обхода волны по углу 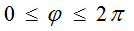вдоль любой параллели шара радиуса r0 равно целому числу 2kr0 полупериодов 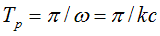колебаний плотности физического вакуума и напряженности электрического поля, которая сохраняет знак на последнем нечетном полупериоде, равный знаку заряда.

Заметим, что полученное решение можно интерпретировать как бифуркацию из спиральной волны фотона с длиной волны λ=2π/k и радиусом окружности r0=1/k, так что его длина волны равняется периметру окружности (см. электродинамику физического вакуума). При столкновении с препятствием и сжатии фотона возникают решения системы уравнений физики элементарных частиц в виде двух волн сжатий-растяжений плотности физического вакуума, распространяющихся по углу φ в противоположных направлениях с ρ=ρ0+q0ei(ωt±kr0φ) и V=0. Тогда рождение любой элементарной частицы можно рассматривать как ее бифуркацию из периодического решения, соответствующего сжатому фотону с некоторой длиной волны. При этом длины волн рождающихся периодических решений (частица и античастица) в полуцелое число раз меньше длины волны соответствующего фотона.

Можно показать, что так определенные электрическое поле и заряд элементарной частицы удовлетворяют на экваторе сферы радиуса r0 уравнению электрона Дирака в электромагнитной форме:


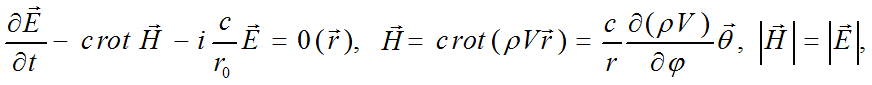
где вектор магнитного поля является виртуальным вектором, так как направлен по углу 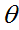, а компонента вектора скорости 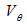по этому углу равна нулю. То есть реально магнитного поля элементарной частицы не существует. Из второго уравнения системы уравнений физики элементарных частиц также легко получить, пренебрегая гравитационным слагаемым, волновые уравнения второго порядка относительно вектора :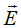

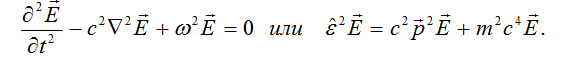
где 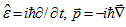- операторы энергии и импульса, а 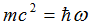. Таким образом, мы приходим к пониманию физической сущности волновой функции ψ в уравнении электрона Дирака в биспинорной форме - это вектор электромагнитной волны частицы, причем магнитное поле в нем является чисто виртуальным. При этом важно отметить, что направленное по радиусу внешнее электрическое поле элементарной частицы, порождается ее электрическим зарядом, но сам заряд является дивергенцией совсем другого внутреннего поля частицы, представленного вторым слагаемым в третьем уравнении системы физики элементарных частиц и направленного по углу 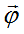. Отметим также, что напряженность электрического поля вне частицы убывает с расстоянием от центра частицы как 1/r2, что соответствует закону Кулона, но внутри частицы (т.е. в шаре радиуса r0 ) напряженность реального (а не линеаризованного) электрического поля убывает как 1/r(!), что решает проблему бесконечности энергии и массы элементарных частиц.

Найдем теперь внутреннюю энергию ε элементарной частицы, используя формулу для работы, произведенной суммой сил внутренних полей частицы, направленных по углу 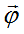, над всеми зарядами, определяемыми дивергенцией этого суммарного поля:


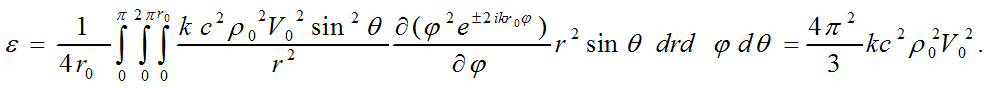
Теперь, чтобы получить основные формулы и соотношения квантовой механики, достаточно обозначить массу элементарной частицы выражением 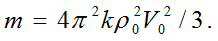После этого немедленно получаем: формулу внутренней энергии Эйнштейна ε=mc2, значение приведенной постоянной Планка 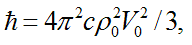формулы энергии и импульса волн де Бройля 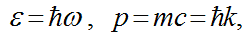формулу для спина элементарной частицы 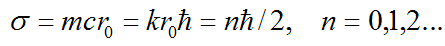, приближенное значение постоянной тонкой структуры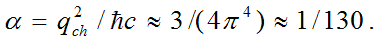

Полученные исключительно методами классической механики формулы полностью совпадают с известными формулами квантовой механики, и, вместе с тем, раскрывают физическую сущность заряда, массы, энергии и спина элементарных частиц, позволяют понять природу протекающих в микромире квантовых процессов. Внутренняя энергия частицы действительно пропорциональна квадрату скорости света, а коэффициент пропорциональности (масса частицы) линейно растет с ростом волнового числа k , а также частоты ω породившего частицу фотона. Постоянная Планка действительно является константой, зависящей только от характеристик физического вакуума и не зависящая от вида элементарной частицы. Спин любой элементарной частицы действительно принимает исключительно значения, равные целому или полуцелому числу ħ, что позволяет поделить все элементарные частицы на два больших класса: бозоны и фермионы. Но самым удивительным и невероятным является практически точное совпадение значения постоянной тонкой структуры α с ее экспериментально найденным значением, равным 1/137.

Отметим, что геометрически более сложным многооборотным элементарным частицам соответствуют более высокочастотные волны сжатия и растяжения плотности физического вакуума, имеющие большую массу и энергию. Естественно предположить, что наиболее простыми полуоборотными частицами со спином 1/2 при n = 1 является пара «электрон-позитрон». Таким образом, электрон является циклом периода два по отношению к исходному циклу, задаваемому движением спиральной волны фотона. Здесь мы приходим к еще одному доказательству справедливости представленной теории – это интерпретация принципа Паули, из которого следует, что электрон возвращается в исходное состояние только при повороте на 720, а не на 360 градусов. Согласно Р.Фейнману принципу Паули удовлетворяет частица, имеющая топологию листа Мёбиуса. Но в универсальной теории динамического хаоса Фейгенбаума-Шарковского-Магницкого (ФШМ), результаты которой справедливы для всех нелинейных систем дифференциальных уравнений макромира, усложнение решений начинается именно с бифуркации удвоения периода исходного сингулярного цикла, причем родившийся цикл удвоенного периода лежит именно на листе Мёбиуса вокруг исходного цикла! Другими словами, электрон – это первая, простейшая бифуркация удвоения периода из бесконечного каскада бифуркаций в соответствии с теорией ФШМ. Из этого следует, что универсальная теория ФШМ работает не только в макро- , но и в микромире, и что найденные здесь элементарные частицы далеко не исчерпывают всего бесконечного набора элементарных частиц, которые могут появиться в результате бифуркаций в нелинейной системе уравнений динамики физического вакуума. Можно предсказать существование у этой системы уравнений и более сложных непериодических решений, являющихся сингулярными аттракторами в смысле теории ФШМ. Таким образом, попытки экспериментального обнаружения как наиболее простой (самой элементарной), так и наиболее сложной из элементарных частиц являются абсолютно бесперспективными.

Отметим также, что так как длина волны электрона в два раза больше длины волны породившего его фотона, а частота колебаний в два раза меньше, т.е. ωph=2ωe то из уравнения сжатого фотона следует, что в окрестности экватора сферы радиуса r0 имеет место уравнение Шредингера


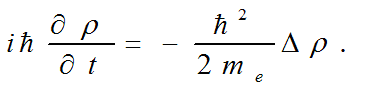
То есть уравнению Шредингера удовлетворяет распространяющаяся по углу φ волна сжатий – растяжений плотности физического вакуума в окрестности экватора сферы элементарной частицы. При этом становится ясным физический смысл ψ - функции в уравнении Шредингера – это плотность физического вакуума.
Уравнению Шредингера удовлетворяет также скалярная функция напряженности электрического поля элементарной частицы.